When I was in the early years of primary school, the kids were provided with
a cardboard container of milk at recess time. Although not a milk-drinker
myself, I was intrigued by the shape of the containers - triangular pyramids
known as "tetra-packs".
At some point, I probably made one out of cardboard, although I can't really
be sure. So here was a shape whose faces were all equilateral triangles. Of
course, I was familiar with cubes (who isn't?), in which the faces were all
squares.
In early high school mathematics classes, the concept of an angle was
introduced; and shortly thereafter, other interesting shapes like pentagons
and hexagons appeared in textbook problems. By second-year high school, it
had occurred to me to wonder if it might be possible to make a solid object
whose faces were all regular pentagons.
I cut some pentagons with edge lengths of one inch and internal angles of
108 degrees out of cardboard, and started to stick them together with sticky
tape. You may bet I was surprised and delighted to find that twelve of these
improbable shapes did indeed enclose space. How about that?!
Subsequently, I found out that it was possible to make two other symmetrical
3-D shapes whose faces were equilateral triangles, one with eight faces (the
octahedron) and one with twenty faces (the icosahedron). These, together
with the tetrahedron (the basis for the "tetra-pack" milk carton), cube, and
dodecahedron (the one with the pentagon faces) formed the only five
polyhedra whose faces were all convex regular polygons of the
same type.
It's not possible to make a regular polyhedron from regular hexagons,
because the internal angles are all 120 degrees - one-third of a full
revolution. You simply get an infinite honeycomb pattern. With regular
polygons of seven sides or more, things are even worse - internal angles are
all greater than 120 degrees, so that you can't stick three of them
together at all without bending them. (Try it if you don't believe me!)
There are any number of excellent websites about polyhedra, which give good
explanations - with pictures - of these five "Platonic solids" (named after
the Greek philosopher and mathematician
Plato, who investigated them.) Rather than "re-invent the wheel" and present
them all here, I'll refer you to
this web-page,
which does it as well as any, and suggest that you have a look at it before
moving on if you're not familiar with these solids.
Right-click
here
to download the BASIC source code - or
here,
to obtain a compiled .EXE version.
(Note: There's always a chance that .EXE files can pick up viruses in their
travels over the internet. To be on the safe side, you might like to run a
virus check after downloading this, before running it.)
I became aware that it was possible to make some polyhedra using more than
one kind of polygon. Perhaps the most common example of this is the
polyhedron which forms the basis for the modern soccer ball; this is made
from twelve pentagons and twenty hexagons. But my knowledge in this area
remained static until late 1974, when I found in the University of Tasmania
bookshop (Hobart) a book entitled "Polyhedron Models", by Magnus J.
Wenninger. This delightful and remarkable book had instructions for building
some 119 different models - and it was quite clear that this was only the
beginning! There are vastly more possible polyhedra than are
presented in the book.
Before continuing, may I encourage you to visit
Magnus J. Wenninger's website
and have a good look around. This man has made an enormous
contribution to polyhedron lore, and has himself made some very significant
discoveries in the field (click
here
to read more about this). He is a (if not the) world authority on
the subject. Don't miss this.
Many thanks to the book's author for permission to include this scan here -
and also for drawing my attention to an error in the original version of
this page.
There are thirteen semi-regular, or uniform, polyhedra whose faces
are also regular polygons, but of two or more different types. (The soccer
ball is based on a uniform polyhedron called a "truncated icosahedron".)
Actually, two of these "Archimedean solids" (named after Archimedes, the
first recorded streaker in history) have non-identical mirror-images; in
that sense there are fifteen different ones - but in a "basic" sense, there
are thirteen.
Again, rather than present them here, I recommend that you visit
this web-page
(part of the same website as the Platonic solids link given earlier) to
familiarize yourself with them.
Having presented the Platonic and Archimedean solids, Magnus J. Wenninger
goes on to discuss the process of stellation, and give some examples.
The basic idea is that you extend the faces of a polyhedron outwards. The
resulting planes may, or may not, meet in such a way as to enclose more
space, which then becomes part of the inside of a new polyhedron.
With the simplest polyhedron - the tetrahedron - this doesn't happen. The
planes diverge, and no new space is enclosed.
With the cube, you get three pairs of parallel planes - which also don't
enclose any more space.
However, with the octahedron, things start to get a bit more interesting.
If you'd like to see this from different angles and elevations, and also
zoom in or out, right-click
here
to download my DOS BASIC program - or
here,
to obtain a compiled .EXE version.
(Note: As mentioned above, there's always a chance that .EXE files can pick
up viruses in their travels over the internet. To be on the safe side, you
might like to run a virus check after downloading this, before
running it.)
On
this page
- another page from the same website mentioned above - about halfway down,
you will find a very attractive picture of this polyhedron.
The stella octangula (which was discovered and named by the astronomer
Johannes Kepler
, 1571-1630) is the only possible stellation of the regular octahedron; if
the face-planes are extended further, no more space is enclosed.
With the regular dodecahedron, things become even more interesting. There
are three possible stellations. The first is known as the small stellated
dodecahedron. Here is my model:
The other two are the great dodecahedron, and the great stellated
dodecahedron (this polyhedron is featured on the cover of "Polyhedron
Models" - see above.) For more information about these, and to gain a deeper
appreciation of the stellation process, see
this page.
You can think of the small stellated dodecahedron as a dodecahedron with a
pentagonal pyramid attached by its base to each of the dodecahedron's
pentagonal faces. Each of the dodecahedron's faces has grown into a
pentagonal star, or pentagram; these intersect each other along the
edges of the original dodecahedron, giving the whole polyhedron the
appearance of a solid star. (This makes a very attractive Christmas tree
ornament.)
Normally, when making polyhedra, to get the best results it's a good idea to
make each small flat piece separately, with tabs on each edge. (If you want
to have the pieces made from differently-coloured cardboard, of course, this
is essential.) These tabs are folded so that they will disappear inside the
model when glued together.
In the case of the small stellated dodecahedron, however, this approach
gives a result that is not quite as rigid as we'd like.
You can make a dodecahedron first, and then make the pentagonal pyramids and
glue them on one at a time - but this tends to make the joins less tidy, and
detracts from the appearance of the final result. When building my model, I
achieved the best of both worlds by making just the pyramids, but
reinforcing each by gluing a pentagon (slightly smaller than the pyramid's
base) with tabs a short distance inside it, and then gluing the pyramids
together by means of tabs at their bases. This produced a sturdy,
attractive polyhedron.
Here are two more views of the model:
(Yet another photograph of this polyhedron is featured at the top of the
page.)
There is a sense in which this polyhedron is regular, just as the
Platonic solids are - except that it's non-convex. If we accept the
pentagram as a (non-convex) regular "star polygon", with five "true"
vertices (the sharp corners) and five "false" vertices (where the sides
intersect), then we can accept the small stellated dodecahedron as a regular
"star polyhedron" in a similar way.
As it turns out, there are just four non-convex regular polyhedra. Three of
them are the stellations of the dodecahedron (mentioned above); the fourth
is the great icosahedron, a stellation of the regular icosahedron.
These four polyhedra are collectively known as the Kepler-Poinsot
solids. Visit
this page
to read more about them and see some excellent diagrams; also
here.
To read about the 59 recognized stellations of the icoshahedron, and view
excellent photographs and graphics for each one, visit
this website.
Note that the icosahedron itself is number 1 in this list; and the great
icosahedron is number 54.
Of course, it's possible to apply the stellation process to polyhedrons
other than the Platonics. The Archimedeans are fair game, for a start!
In "Polyhedron Models", Magnus J. Wenninger presents some stellations of two
of the Archimedean solids: the cuboctahedron and the icosidodecahedron. Some
are not particularly exciting; but there are some gems among them.
In 1975, I decided to stellate the simplest Archimedean solid: the truncated
tetrahedron.
The idea of "truncating" a polyhedron is that you cut off bits in such a
way as to remove some vertices and create new ones, leaving behind another
polyhedron with some significance in its own right. Each of the Platonics
can be truncated to produce one of the Archimedeans. (I've already mentioned
the truncated icosahedron - the "soccer-ball polyhedron.")
With the tetrahedron, we make cuts one-third of the way along each edge so
as to remove each of the four vertices, replacing it with three new ones.
The resulting polyhedron has four regular hexagonal faces (remnants of the
original triangles), and four small triangular faces (where the cuts were
made). It looks somewhat like a deformed octahedron. (Click
here
to see a model, as well as instructions for making one of your own. Also,
have a good look around this website: lots of good practical
polyhedron information here, as well as links to other excellent sites.)
This polyhedron can be stellated. If we produce the hexagonal faces, of
course the result will be to "grow back" the original tetrahedron (i.e.
before the truncation). However, it's when we produce the small triangles
(the actual truncations) that things start to become more interesting.
My original model got squashed at some point. However, some years ago I made
a replacement. Here are some photographs (click on them to see bigger
versions):
As you can see, the stellation process applied to the hexagons has not only
restored the original tetrahedron's four triangular faces, but it has also
grown them out to make four other triangles of the same size - so that the
eight triangles appear, in coplanar compound pairs, as four six-pointed
stars.
Additionally, the four small triangles which are the result of the
truncation have grown out to meet these four new triangles and each other,
producing large triangles with "bits missing" at the centres of their sides.
In three dimensions, these missing bits translate into small tetrahedral
"gaps", one at the centre of each of the six edges of a new, large
tetrahedron.
Here's a little problem for you:
What proportion of this solid's volume is occupied by the truncated
tetrahedron at its centre?
Note: This problem can be solved without knowing the formula for the
volume of a pyramid, or even the formula for the area of a triangle. With a
little bit of insight, you may be able to solve it quite quickly.
(You can click
here
to see the answer - but give yourself a reasonable chance of working it out
before doing so!)
The polyhedron just discussed is the first stellation of the
truncated tetrahedron. It's possible to stellate it once more; the effect of
doing this will be simply to fill in the gaps in each of the six edges of
the large tetrahedron, so that the resulting polyhedron will be a compound
of a small tetrahedron and a large one.
We've looked at regular polyhedra - those whose faces are identical
regular polygons, and whose vertex cross-sections are also identical regular
polygons. These are the (convex) Platonic and (non-convex) Kepler-Poinsot
solids.
Also, we've considered a group of uniform polyhedra - the
Archimedean solids. These are all convex; their faces are regular polygons
of two or more types. (Their vertex cross-sections are identical, but they
are not regular polygons.)
Two other classes of uniform polyhedra are the uniform prisms and
antiprisms.
Uniform prisms are polyhedra which have a pair of parallel faces which are
regular polygons (the "top" and "bottom" faces) which are joined together by
means of squares (the "sides").
One of the Platonic solids - the cube - may be viewed as a square prism. Its
"top" and "bottom" faces are - like its sides - squares.
Clearly, there are infinitely many of these. The simplest is the triangular
prism; but there is no limit to the number of sides a prism may have.
The antiprisms are perhaps somewhat more interesting. Like the prisms, the
"top" and "bottom" faces are identical regular polygons; but this time, they
are linked by equilateral triangles rather than squares.
To make a pentagonal antiprism, for example, you need two identical regular
pentagons. Attach five equilateral triangles around each, one attached to
each edge. On one of the resulting shapes, bend the triangles upward;
this becomes the "bottom" half of the model. On the other, bend the
triangles downward; this becomes the top half of the model. Then
connect the two halves by gluing together the free edges of the two sets of
triangles in a zigzag fashion.
Just as the cube can be viewed as a square prism, so the octahedron can be
viewed as a triangular antiprism - the simplest antiprism. Like the prisms,
there are infinitely many possible antiprisms, with the "top" and "bottom"
polygons having any desired number of sides.
Antiprisms can somewhat resemble drums, in which the drumheads are held taut
by a rope zigzagging around the drum, giving the appearance of triangles.
Such polyhedra are moderately interesting - as long as the tops and bottoms
are convex polygons. However, if these are non-convex, both prisms and
(especially) antiprisms acquire much more appeal.
The simplest star-polygon is the pentagram (see the small stellated
dodecahedron above). A pentagrammic prism (some sources use the term
pentagrammatic) has its pairs of pentagram arms linked by rectangles,
in such a way that two of them in the same plane represent the visible parts
of a square which cuts through the solid.
A pentagrammic antiprism is immediately far more interesting. The triangles
cut through the interior of the polyhedron, as well as through each other.
To see a picture of one, click on
this link;
also
this link.
There's more to be said about this! Click on
this link
to see a quite different pentagrammic antiprism (a crossed pentagrammic
antiprism, in which the triangles cut across internally to link the tops
and bottoms, thus bringing them closer together and creating a very
intricate structure where the triangles intersect each other.)
Now: click on
this link
to see (among other things) an octagrammic antiprism.
In the mid-1980's, I made one of these. Here it is (you can click on the
photographs to see slightly bigger versions):
There is one other class of uniform polyhedra: the non-convex uniform
polyhedra.
There is a sense in which the non-convex prisms and antiprisms just
described fit this description. However, in much the same way that the
Kepler-Poinsot solids are non-convex analogues of the Platonic solids, there
are 53 uniform polyhedra which are non-convex analogues of the Archimedean
solids. (The last of these was discovered only in 1954.)
In "Polyhedron Models", Magnus J. Wenninger goes into considerable detail
about them, giving detailed instructions on how to make models. Some of them
are incredibly complex. Unlike the Kepler-Poinsot solids, which are all
stellations of Platonic solids, none of these 53 is a stellation of either
a Platonic or an Archimedean solid (although there are some surprising
similarities).
I'll present just one of them: the great cubicuboctahedron. (You can
click on these photographs to see bigger versions.)
This poor old thing is rather the worse for wear. I made it in the early
1990's, and since then it has graced my living-room pelmet (along with
other polyhedra). At some stage, a few years ago, I noticed that there were
some small holes in the brown parts. Since then, these have become much
worse; in some parts, there is little more than a lace-work of fibres left.
Some nasty little insect with a taste for brown cardboard has been "at it"!
What you see here are the best views I could get of the model. (Several of
my other polyhedra have suffered a similar fate.)
Also, the edges are starting to come apart. Perhaps I didn't use enough
glue. (I can see myself having to replace this polyhedron someday.)
It's a "moderately" complex example of its class. It has six octagrammic
faces in the planes of a cube; six square faces, behind and parallel to the
octagrams, cutting through the interior of the polyhedron to enclose a small
cube at its centre; and eight equilateral triangular faces, in the planes of
an octahedron, which cut through each other and the square faces to produce
gaps along the edges (somewhat similar to those in the first stellation of
the truncated tetrahedron, above) and dimples at the corners.
It has a point of interest which I've never seen mentioned anywhere else,
related to space-filling.
Cubes can "fill space", in the sense that you can stack up as many as you
like (of the same size) to fill a volume. (This, of course, is why volumes
are measured in cubic units.)
The cube is the only single Platonic solid that can do this, although it is
possible to fill space with a combination of octahedra and tetrahedra. Among
the Archimedeans, there is just one which can be used on its own: the
truncated octahedron. (There are ways to use some Archimedeans in
combination with other polyhedra to fill space. I'll leave that as "an
exercise for the reader": see what you can find out about it!
Update, Saturday 11th July 2009:
I've just stumbled across a page about truncated octahedra which has some
rather good graphics showing how they can fill space both on their own and
in combination with other polyhedra; click
here
and scroll down toward the bottom of the page.)
There is one other kind of polyhedron which will fill space by itself: the
rhombic dodecahedron. This is the
dual
of the Archimedean solid known as a cuboctahedron.
This link
contains animations of both of these.
The great cubicuboctahedron is of interest in this regard because, if we
think of it as a faceted cube (i.e. a cube with "bits missing"), and
stack a number of them as we would with cubes in the usual space-filling
way, the missing bits at their edges combine to make octahedral holes in the
overall structure, and those at their corners combine to make holes in the
shape of truncated cubes. Thus, we have here a set of three polyhedra - two
uniform and one regular - which together will fill space.
Just thought you'd like to know!
One more thing: the numbers of great cubicuboctahedra, truncated cubes, and
octahedra (respectively), required to fill space, are in the ratio 1:1:3.
(Can you see why?)
Finally, some compounds.
There are many possible compounds of polyhedra. We've already mentioned the
stella octangula, which is a compound of two identical tetrahedra. Also, the
second (and final) stellation of the truncated tetrahedron is a compound of
two tetrahedra of different sizes.
Among the 59 stellations of the icosahedron is a compound of five octahedra
(number 3 in the list mentioned earlier). There is also a compound of five
tetrahedra (number 17) and a compound of ten tetrahedra (number 12). The
compound of five tetrahedra can exist in two non-identical forms, which are
mirror-images of each other; the compound of ten tetrahedra - which is
symmetrical - is the compound of these two.
Remember the principle of duality, mentioned above? If we replace each
octahedron in the compound of five octahedra with its dual - a cube - we get
a
compound of five cubes.
(A cube itself may be rather boring; but this compound of five of them is
beautiful. It may be viewed as a faceted dodecahedron.)
Of course, it's possible to make a compound of any polyhedron and its dual.
The stella octangula can be thought of this way, since a tetrahedron is
"self-dual"; and it's possible to make a compound of a cube and an
octahedron, and a compound of a dodecahedron and an icosahedron.
It's possible to make a compound of two dodecahedra! Here's mine (you can
click on the photos to see bigger versions):
I made the pink one first, and then made twelve identical blue low pyramids,
with tabs folded under, and stuck them onto the pink dodecahedron, one to
each face. As you can see, it looks a bit untidy; I would probably have
obtained a better result if I had made twelve low pyramids of each colour
and then stuck them together. (I alluded to this issue earlier, with
reference to the construction of a small stellated dodecahedron.) This model
has overall cubic symmetry; it can be viewed as a cube with a "roof" on each
face.
It's also possible to make a compound of three cubes with overall cubic
symmetry (again, you can click on these to see bigger versions):
- and last, but by no means least, its lovely dual - a compound of three
octahedra (again, click on the pictures to see bigger versions):
That'll do! Enough there to whet your appetite, methinks. If you'd like to
see more about polyhedron compounds, I recommend the following links, among
which you will find things mentioned in this page and plenty more besides:
http://www.uwgb.edu/dutchs/symmetry/polycpd.htm
http://mathworld.wolfram.com/Octahedron3-Compound.html
http://www.korthalsaltes.com/polyhedra_compounds.html
Sometimes, you hear interviews with people who say that they've spent all
their lives listening only to one kind of music - probably, the popular
music of their era. Then, one day, they stumble across something by
Beethoven, or Mahler, or Rachmaninov - and it's as though a curtain goes up
in their mind. Suddenly, what they've always thought of as the
old-fashioned, stuffy world of "classical music" is seen in a new light; and
things are never the same again.
Mathematics can be like that. People who hated maths in school (probably for
all the wrong reasons) may begin to see its true nature, and want to get
involved with it.
Is that you? If so, may I suggest that there is probably no gentler, more
obviously friendly way to start than by making polyhedra. You can begin with
the simple ones, develop some understanding of the geometry and trigonometry
involved, and gradually expand your horizons. Best of all, you'll find
yourself producing beautiful ornaments which, with care, will last for
decades. And it's cheap! Cardboard, scissors, and glue, basically.
The field is huge, and there's an enormous amount of
information available on the internet.
This website
is very attractive, and contains lots of useful information and links to
other web-pages on the topic. (Perhaps you could eventually make a
contribution, by featuring some of your own models on your own website?)
You might also consider visiting the local library to see if they can obtain
Magnus J. Wenninger's books for you (he has written several), or other books
on the subject. ("Mathematical Models" by H. Martyn Cundy and A. P. Rollett
is excellent in this regard.)
Happy hunting!
My home page
Preliminaries (Copyright, Safety)
Polyhedra: frozen music for the eyes
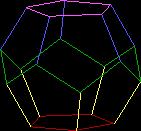Actually, there is one Platonic solid-related thing on this page that you
can download: a DOS BASIC program I wrote which shows a regular
dodecahedron, and allows you to rotate it so as to see it from different
angles and elevations, and also to zoom in or out. (The diagram at left is
from a screen-shot of this program running.)
Of course, I bought the book at once. It has provided me with many happy
hours of reading in the intervening three decades; and I have made several
of the polyhedra featured in the book - as well as some I've found in other
publications, and some I've worked out for myself. In this page I'll present
just a few of these.
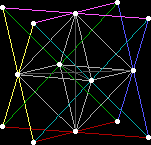
This diagram shows an octahedron (grey), which has been stellated. The
coloured lines show where the resulting extended planes intersect to enclose
eight small triangular pyramids (tetrahedra). The resulting entire structure
is a compound of two large tetrahedra, i.e. these tetrahedra are "stuck
through each other".
Return to Mathematical stuff menu