
In space, distances can get very large.
It's common to measure distances between astronomical objects in terms of
the speed of light in a vacuum. This is very fast - just a whisker under
300,000 kilometres per second - but not so fast that it can't be noticed
under certain conditions; and the fact that it's not even faster can
actually be a bit of a nuisance!
During the Apollo program, conversations between Earth and astronauts on the
moon sounded somewhat stilted, as if the participants were slow-witted and
finding it difficult to think of anything to say. Obviously, this was not
the case; the illusion was caused by the fact that the moon is far enough
away (384,400 kilometres) so that light (and radio-waves, which travel at
the same speed) takes a perceptible time to make the journey (about 1.28
seconds).
So if a person on Earth speaks to an astronaut on the moon, and the
astronaut replies immediately, the person on earth will notice an apparent
hesitation of about two and a half seconds. Of course, the astronaut will
notice a similar delay.
Even at the geostationary orbit, in which a satellite travelling from west
to east over the equator will stay at the same position above the Earth, the
time-delay can be noticeable. This orbit is about 36,000 kilometres above
the Earth, so that light (or a radio signal) will take about 0.12 second
(about an eighth of a second) to cover the distance. If a reply is sent
immediately, the round trip thus takes about a quarter of a second. This is
not enough to be a real problem for speech, but for communication between
electronic signalling systems, which communicate by "hand-shaking" (several
back-and-forth messages to ensure that a signal arrives correctly), it's a
real drag.
The distance from the Earth to the sun is about 150 million kilometres. Thus
light from the sun takes (150 million / 300 thousand) seconds, i.e. 500
seconds, or eight and a third minutes, to reach the Earth. So we can say
that this distance (also known as an "astronomical unit", AU) is eight and a
third light-minutes.
- Which brings us to the idea of a light-year. One year is
365.25 × 24 × 60 × 60 = 31,557,600 seconds
so that a light-year is 31,557,500 / 500 = approximately 63,115 AU, or 9.467
trillion (million million) kilometres.
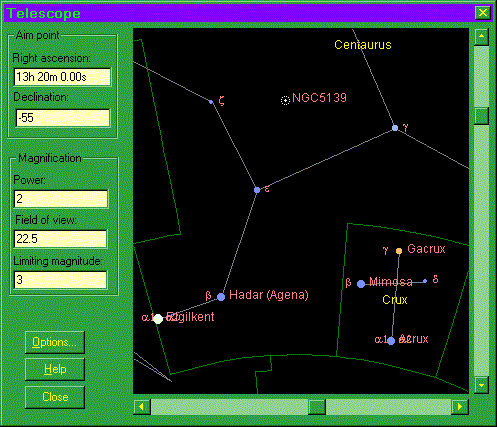
In the Southern Hemisphere, we can see a very striking constellation called
Crux, or the Southern Cross. It consists of four stars arranged somewhat
like a kite. Close by are two stars known as the "pointers", Alpha Centauri
and Beta Centauri (both part of another constellation, Centaurus).
The following graphic of the Southern Cross and its pointers was obtained
using the planetarium program
Home Planet
:
The Cross is at lower right. The pointers are to its left. The further
pointer from Crux, Alpha Centauri, is the bright star at the lower left
corner of the graphic. It is the closest star to the Earth (other than the
sun, of course - duh). Alpha Centauri is also known, by navigators,
as
Rigel Kentaurus
- or simply Rigel Kent (labelled as Rigilkent on the
graphic).
So, if Alpha Centauri is the closest star to us, just how far away is it?
It's not "close", in any sense of the term that we can easily relate to!
It's 4.35 light years away. A quick check with a calculator shows that this
is a distance of well over a quarter of a million AU!
Actually, Alpha Centauri is not a single star. In fact, it's a three-star
system. Click
here
to see an interesting web page which goes into some detail. Also,
this page
is well worth a look.
Two of the Alpha Centauri stars are of comparable size and brightness to our
sun, and orbit their common centre of mass. The third star, a red dwarf, is
quite a lot further out. Presently, it's the closest of the three to Earth -
which is why it's called "Proxima Centauri".
Just before moving on - see that funny-looking white thing called NGC5139 in
the above graphic near top-centre? That's a globular cluster - one of
a number of such more-or-less spherical aggregations of stars around the rim
of the Milky Way. It's also known as Omega Centauri, and is about 16
thousand light years away. Click
here
to read more about it and see a photograph.
Other pages, with photos, about this interesting object are
here
,
here
, and
here
. (That last page has lots of other interesting pictures too - have a good
look around.)
A different unit, the parsec, is another useful way to measure
astronomical distances; and this one doesn't require any mention of the
speed of light. Apparently, astronomers prefer this unit. If you're a
science-fiction buff, chances are you may have seen it mentioned, possibly
without knowing exactly what it means.
The term is a short form of "parallax second". The "second" here is not a
unit of time, but a second of arc - a small angle.
To get an idea of how small this angle is, think of it in terms of latitude.
The Earth has a radius of about 6,400 kilometres, and a diameter of twice
that - 12,800 kilometres. Then the circumference is that figure times pi
(approximately 3.1416), or 40,212 kilometres. So one quarter of this -
10,053 kilometres - is the distance from the equator to either pole. This is
a latitude shift of 90 degrees, i.e. 90 × 60 × 60 = 324,000 seconds of arc.
So one second of arc corresponds to a distance of 10,053 / 324,000 = 0.031
kilometres, or 31 metres - quite literally, a stone's throw.
Now, consider what a second of arc means on an astronomical scale. Imagine a
vastly bigger sphere in which one second of latitude corrsponds to a
distance, on its surface, of 1 AU. So we're scaling up by a factor of 150
million divided by 0.031, i.e. about 4.84 billion (thousand million).
If we scale up the radius of the Earth (6,400 kilometres) by the same
factor, we get about 31 trillion (million million) kilometres for the radius
of our big sphere. That distance is one parsec.
Now, recall that a light-year is about 9.467 trillion kilometres. Dividing
31 by 9.467 gives a figure of about 3.27, which is thus the number of
light-years in one parsec.
Admittedly, we've been approximating perhaps more than we should have been,
in reaching this figure. Still, the result is not bad: the accepted figure
is 3.259 light-years.
Finally, also recall that Alpha Centauri is 4.35 light-years away. Dividing
this by 3.259 gives 1.335. So our nearest stellar neighbour is about one and
a third parsecs away.
The discussion just given involves one way of visualizing a parsec (which I
hope has been helpful, in reducing it to things we can more easily get our
heads around).
There are other, equivalent, ways to understand what a parsec is, and to
calculate its size (although, of course, any such calculations end up simply
being "variations on a theme", and giving the same result). Here are some
links which deal with these:
http://www.physics.hku.hk/~tboyce/sfseti/A6parsec.html
http://www.tiscali.co.uk/reference/encyclopaedia/hutchinson/m0005746.html
http://www.astronomynotes.com/starprop/s2.htm
http://ourworld.compuserve.com/homepages/bmoler/litetime.htm
My home page
Preliminaries (Copyright, Safety)
Distances in space

(This gives you a chance to see the weird colour scheme I like on my
computer!  )
)



 Return to Astronomical stuff menu
Return to Astronomical stuff menu

