
Click on the picture to see a 640 x 480 pixel version.
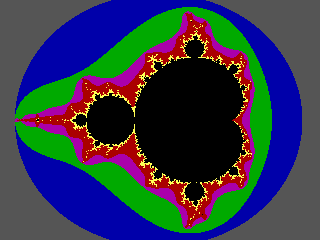
The black part of the picture above is the shape that appeared in blotchy
ink in a printout produced by Dr. Benoit Mandelbrot in the late 1970's, on
what we would now consider to be primitive computer equipment.
Within a few years, it became possible for the amateur programmer to produce
attractive patterns based on this shape, complete with the splashes of
colour around the outside which occur where points are not quite in
the black part now known as the Mandelbrot set. For more detail on this,
click
here
to see my Word 97 document "Introduction to the Mandelbrot Set".
NOTE:
There is always a chance that Word documents may pick up
viruses or other nasties in their travels over the internet. Please see the
suggestions on my
home page
under SECURITY before downloading this if you have any doubts.
My purpose in creating these pages is twofold: firstly, just to share some
of the M-set pictures I've created using simple programs; and secondly, to
attempt to help the aspiring novice to make a start in doing much the same
sort of thing.
Altough there are many web-pages with M-set graphics and information about
the historical background, I haven't seen many which attempt to provide a
simple, practical introduction to the actual programming processes involved.
So I'd like to think I'm meeting a need.
Each of the pages in this collection presents one or more images of a
particular region of the M-set. For each image, I've made available a link
for you to download the BASIC source code which produced that image.
Some of these programs have little "bugs" in them! Don't worry - they're not
nasty things like viruses; just little imperfections that I put in by
mistake when preparing them which make things not quite 100% efficient
(although they don't cause any actual inaccuracies). I did iron out some of
the bugs as I went on, and I also made other little alterations and
improvements along the way. This process in itself was a journey for me.
You can right-click
here
to save the source code for this first graphic (640 x 480 pixel version).
Also, for this first one only, I've decided to present the program written
out in full within this page, with a few comments, just to get you started.
Here it is:
SCREEN 12
iterationlimit = 100
colour0 = 14
ylow = -1.25
FOR i = 0 TO 480
a$ = ""
Comments:
As you can see, it's quite short and simple. Although the Mandelbrot set
itself is very complicated, the rules which generate it are not.
Here are some explanations of things within the program:
SCREEN 12 puts the computer into 640 x 480 pixel graphic mode. The
background is black.
iterationlimit is the maximum number of iterations permitted before the
program decides that a particular point doesn't "escape", and is thus in the
M-set. Note that the value is set to 100 for this "whole-set" run; that's
quite adequate. As mentioned elsewhere, I generally used 1,000 for most of
the other runs, with 10,000 being used when I wanted really fine detail (but
that wasn't necessary very often).
The colours are as follows: 14=yellow; 4=red; 5=magenta (port wine colour);
2=green; 1=blue; 8=dark grey; and 0 (the colour plotted for points in the
M-set) is black (in keeping with "tradition").
ylow and yhigh are the values represented by the bottom and top of the
screen, respectively. I've set these values to -1.25 and 1.25, respectively,
for this "whole M-set" run. The entire M-set lies in a circle of radius 2,
centred on the origin - well within these vertical limits.
xlow is the value represented by the left-hand edge of the screen, chosen to be
-2.15 for this run. I've arranged for the computer to calculate xhigh, the
value represented by the right-hand edge of the screen, bearing in mind that
the picture will have an "aspect ratio" of 4 to 3 (i.e. its width is 4/3
times its height). As it turns out, xhigh is 1.183333... (recurring, but of
course rounded off by the computer). The entire M-set is within these
horizontal limits.
Now we come to the main part of the program, the "engine room" which
actually calculates the colour values and plots the points - and here we
come to our first bug!
The FOR statements should be FOR i = 0 TO 479 and FOR j = 0 TO 639,
respectively. This is because there are 640 pixels (dots) across the screen,
numbered from 0 to 639, and 480 dots down the screen, numbered from 0 to
479. So the commands for when i = 480 and j = 640 don't actually do
anything. (Silly me!)
To understand the calculating and plotting process in detail, please refer
to the document linked to above. (I'll just mention here that the condition
in the program about rsquared being greater than or equal to 4 has to do
with the circle of radius 2 which completely surrounds the M-set, as
mentioned above. Click
here
to see a 480 x 480 picture of this.)
In retrospect, I can see that xc and yc aren't really necessary. I could
have left those two statements out, and just used x and y respectively in
the equations for u and v. A minor bug - but no harm done!
The BASIC command PSET (j,i), colour simply plots the particular colour at
the pixel with coordinates j (from the left) and i (from the top).
No doubt you've noted that the program actually plots a black pixel if that
particular location is in the M-set. Strictly speaking, that command is
unnecessary, as the screen starts out all black anyway. However, if you
wanted to make the M-set a different colour from black, you'd need that
command - with the appropriate value of colour being thus plotted at that
time.
The last two statements in the program simply tell the computer to wait
until the user presses the Esc key (at the top left of the keyboard, with
ASCII code 27).
- And that's it! Really quite simple once you've grasped the idea of what it
is required to do.
Now that I've explained the basics, hopefully you'll be able to see how my
programming technique changed (improved?) in later programs, without much
further explanation. The "clever bits" in the program remain essentially
unchanged; it's the details like x and y limits and colour calculations that
change from one program to the next.
You will find another listing, in a later page, for a BASIC program which
generates the components of a movie showing a zoom into an area of the
Mandelbrot set.
My home page
Preliminaries (Copyright, Safety)
Mandelbrot set: Region #1
(the whole set)


colour1 = 4
colour2 = 5
colour3 = 2
colour4 = 1
colour5 = 8
iterationlimitcolour = 0
yhigh = 1.25
xlow = -2.15
xhigh = xlow + (yhigh - ylow) * 4 / 3
FOR j = 0 TO 640
x = xlow + j * (xhigh - xlow) / 639
y = yhigh - i * (yhigh - ylow) / 479
xc = x: yc = y
iterations = 0
rsquared = 0
DO UNTIL rsquared >= 4 OR iterations > iterationlimit
u = x * x - y * y + xc
v = 2 * x * y + yc
rsquared = u * u + v * v
x = u: y = v
iterations = iterations + 1
LOOP
IF rsquared >= 4 THEN
IF iterations > 20 THEN
colour = colour0
ELSEIF iterations > 6 THEN
colour = colour1
ELSEIF iterations > 4 THEN
colour = colour2
ELSEIF iterations > 2 THEN
colour = colour3
ELSEIF iterations > 1 THEN
colour = colour4
ELSE
colour = colour5
END IF
ELSE
colour = iterationlimitcolour
END IF
PSET (j, i), colour
NEXT j
NEXT i
DO: a$ = INKEY$: LOOP UNTIL a$ = CHR$(27)

 Return to
Fractals #1: the Cantor and Mandelbrot sets
Return to
Fractals #1: the Cantor and Mandelbrot sets

