
Oh, no - not another page of Mandelbrot set pictures?
Well, yes, it is - but with a difference. Please bear with me; I think
you'll be pleasantly surprised.
Actually, I don't have a problem if I happen to run across a web-page full
of fractals of various kinds, including Mandelbrot set pictures. In fact, I
go looking for them sometimes. It may be some 20 years since the "M-set"
burst into public consciousness; but I'm still happy to see it. I can't
imagine I'll ever get sick of it.
Although Mandelbrot set graphics are the main thrust of this page, there are
also a few other matters mentioned here by way of introduction. If some of
them encourage you to scratch your brain, I'm doing something right!
[Just while I think of it - if you like the Mandelbrot set, and if you also
like science fiction, may I recommend "The Ghost from the Grand Banks" by
Arthur C. Clarke (Orbit,
1990), in which the M-set plays a key rôle.]
In the early 1980's, there were rumblings in the mathematical/scientific
community that some sort of major paradigm-shift was under way. Our
understanding of how the universe is put together was changing.
A century earlier, in 1883, the German mathematician Georg Cantor had
published a paper in which he described what would come to be known as the
"Cantor set".
Suppose you have a straight line segment. (Usually, we consider the line
segment joining 0 and 1 on the real number line.) Now, remove the middle
third - the bit between 1/3 and 2/3 - but leave the actual points 1/3 and
2/3 behind. Then remove the middle third of each of the two remaining
pieces, again leaving the end-points. This leaves four short pieces. Remove
the middle third of each of these...
If we continue in this way "forever", what is left?
Well, of course, we can't continue forever, because we don't have enough
time.
There are some surprises among those isolated points. You'd expect all the
end-points of the various line-segments generated by removing bits of the
original line to be included - as they indeed are. But there are other
points in there too. Guess what: one of them is the point corresponding
to 1/4 on the number line - and that is very definitely not one of
the end-points! How about that? Can you see which of the tiny line-segments
at the bottom of the above diagram must contain that point?
Even better: Can you prove that 1/4 is in the Cantor set? Spend a bit
of time thinking about it; if you really can't figure it out, you can click
here
to see a proof. (Here's a clue: there's a geometric progression
involved.)
NOTE:
There is always a chance that Word documents may pick up
viruses or other nasties in their travels over the internet. Please see the
suggestions on my
home page
under SECURITY before downloading this if you have any doubts.
The Cantor set is the simplest example of what Benôit Mandelbrot would call
a fractal, in his book "Fractals: Form, Chance and Dimension",
published in 1977 by W.H.Freeman and Company.
Since Cantor's time, many fractals have been "discovered". If you're not
too familiar with the subject, I recommend that you use a WWW search engine
to see what you can find about the following: Koch snowflake curve; Peano
space-filling curve; Sierpinski gasket; Menger sponge; Alexander horned
sphere. The following links are helpful in this regard, and also contain
further information about the Cantor set:
http://en.wikipedia.org/wiki/Cantor_set
http://mathworld.wolfram.com/CantorSet.html
http://mathworld.wolfram.com/TotallyDisconnectedSpace.html
All the fractals mentioned in the previous paragraph are close relatives of
the Cantor set, except perhaps the second - and even then, it's possible to
make a connection. In Scientific American's "Mathematical Games" column, in
the April 1978 issue, Martin Gardner discusses a link between Peano's ideas
and the Koch snowflake curve. Well worth a read if you can find a copy.
During the early 1980's, Dr. Mandelbrot placed the emerging science of chaos
theory and fractals on a firm foundation. Most importantly, he pointed out
that fractals do indeed have a lot to do with nature, from coastlines and
cloud formations to the way plants grow. Appropriately, the most famous and
popular fractal of all, the Mandelbrot set (which he discovered), is named
after him.
The basic concept of a fractal is self-similarity - the idea that if
you "zoom in" (or "zoom out", for that matter), the thing still looks pretty
much the same at any level of magnification. Thus, when you remove the
middle thirds at a particular stage while "generating" the Cantor set, the
result at the next stage looks - well, similar.
The same is true of coastlines and clouds, and also many plants (fern leaves
and broccoli are classic examples). It really does seem to be a law of
nature. In another of his books, "The Fractal Geometry of Nature" (1982),
also published by W.H.Freeman and Company, Mandelbrot develops this theme.
The Mandelbrot set has this self-similar property too. It's fun to zoom in
on parts of it and find - astonishingly - small "almost-copies" of itself
scattered all over the place, each containing even smaller
"almost-copies"...
Great fleas have little fleas upon their backs to bite 'em,
- Augustus de Morgan (1806-1871), in "A Budget of Paradoxes", 1866
(You'll find lots of "fleas" in the pictures toward the bottom of this
page.)
Just before moving on:
In February 1999, Scientific American published an article by Dr. Mandelbrot
entitled "A Multifractal Walk down Wall Street", in which he asserted that
the behaviour of the stock market is essentially chaotic in nature. (Click
here
to see a short review of this article.)
To read more about this obviously important issue, click
here.
You may also be interested to vist my
All that glisters...
page to see some of my thoughts on this and related matters. (That page
also contains a link to the web-page just mentioned.)
In August 1985, in Scientific American's "Computer Recreations" column, host
A.K.Dewdney presented a magnificent article which has probably done more to
make the Mandelbrot set known to a wide audience than any other. To their
credit, Scientific American gave the cover of that issue over to a lovely
graphic of part of the M-set. If you'd like a good introduction,
you can't do better than to obtain a copy. (You can't have mine - it ranks
among my other treasures like "The Boy Electrician" by Alfred P. Morgan,
"Model Making for Young Physicists" by A.D.Bulman, and "Polyhedron Models"
by Magnus J. Wenninger - and you can't have any of those either. Sorry!)
On the other hand, if you'd like a very brief overview of how the Mandelbrot
set "works", you can click
here
to see my own article.
NOTE:
There is always a chance that Word documents may pick up
viruses or other nasties in their travels over the internet. Please see the
suggestions on my
home page
under SECURITY before downloading this if you have any doubts.
As the opening of this page suggests, there are many, many web-pages which
feature fractals - the M-set especially. One of the best is that by
Prof. Clint Sprott,
which features an enormous range of very interesting fractals of many kinds
- highly recommended.
Such graphics are often produced with top-of-the-range programming software
which requires the user to have considerable expertise in its use. Or they
might be generated with dedicated packages like the excellent freeware
program
FRACTINT,
which - though powerful and effective - can't really provide the user with a
nitty-gritty programming experience.
Another way of exploring the Mandelbrot set is by using a dedicated M-set
zoom program. There are quite a few of these around on the net; I recommend
the one by
Rudy Rucker
.
Actually, this is part of a software package inspired by James Gleick's
magnificent book "CHAOS", published in 1988 by Sphere Books. This package,
also entitled "CHAOS", can be downloaded
here
.
It's a DOS package which will run OK under Windows. In addition to the
section on the Mandelbrot set (and variations), there is a host of other
very intriguing modelling programs: a pendulum over magnets; strange
attractors (including the famous Lorenz attractor); fractal landscapes;
various cellular automata (including a "hodgepodge machine", which models
the fascinating Belousov-Zhabotinsky reaction) - and lots more. It's
described as shareware, but there's no cost for its non-commercial use.
You'd be hard pressed to find anything better anywhere.
In common with FRACTINT, CHAOS is still more of a software package than a
"programming language", but can provide you with a neat entry-point into
M-set lore. You can use the Mandelbrot component to hunt around the M-set to
find a region you like, read off its screen coordinates, and then - if
you're so inclined - enter those coordinates into your own M-set program
(feel free to modify mine, presented below) to produce highly customized
views of your favourite regions.
If you've come here by way of my
Mathematically-Based Computer Graphics
sub-menu, you'll know that I live in what some may unkindly call a
time-warp.
("It's just a jump to the left...")
For programming, I prefer good old quick-and-dirty methods like a DOS BASIC
interpreter, in which I can throw something together which is easy to
understand, and which operates in what I regard as a reasonably
non-threatening environment - and I can tweak things to work exactly as I
want. And that's very satisfying!
The rest of this page is dedicated to some of my own M-set examples, with
some discussion of the origin of each one and how it was "massaged" into
something of which I could be proud. As you'll see, there's as much art as
science in generating a really satisfying fractal.
My first attempts to produce Mandelbrot set pictures were done in BASIC on
my old Commodore 64, way back in late 1985. They took ages - each
picture was an overnight run (or even longer, if I was trying to "dig deep"
into the set). However, if I may say so, I obtained some pretty nice
results! (Click
here
and scroll down toward the bottom of the page to see them.)
I "got the bug" (or "flea", perhaps?) to start doing this again, on my PC,
late in 2004.
Here you can see the results. To date (March 2005), I have produced 18
essentially different Mandelbrot set graphics, some with variations. You can
click on the links below to go to a dedicated page for each.
UPDATE, August 2005: three more have been added, taking the total to 21.
UPDATE, April 2006: four more, slotted in so that they are numbers 20, 21,
22, and 23; those previously numbered 20 and 21 are now 24 and 25.
In each of the following pages, you will find BASIC source code for each
graphic, with some discussion of how I adjusted the programs to get just the
effect I wanted at any stage. By clicking on a particular scaled-down
graphic (320 × 240 pixels), you can see the full-size version (640 × 480
pixels).
There's enough here, hopefully, to enable you to get involved in producing
your own Mandelbrot set graphics, with whatever programming system you use
- if you're that way inclined.
Let the journey begin!
Mandelbrot set: Region #1
Mandelbrot set: Region #2
Mandelbrot set: Region #3
Mandelbrot set: Region #4
Mandelbrot set: Region #5
Mandelbrot set: Region #6
Mandelbrot set: Region #7
Mandelbrot set: Region #8
Mandelbrot set: Region #9
Mandelbrot set: Region #10
Mandelbrot set: Region #11
Mandelbrot set: Region #12
Mandelbrot set: Region #13
Mandelbrot set: Region #14
Mandelbrot set: Region #15
Mandelbrot set: Region #16
Mandelbrot set: Region #17
Mandelbrot set: Region #18
Mandelbrot set: Region #19
Mandelbrot set: Region #20
Mandelbrot set: Region #21
Mandelbrot set: Region #22
Mandelbrot set: Region #23
Mandelbrot set: Region #24
Mandelbrot set: Region #25
Earlier in this page, I mentioned Arthur C. Clarke's novel "The Ghost from
the Grand Banks". The book's main theme is an attempt to salvage the
Titanic; but - intriguingly - the Mandelbrot set plays an important part.
The novel was first published by
Orbit
in 1990, soon after the Mandelbrot set became well-known - almost certainly
largely as a result of Dr. Dewdney's previously-mentioned article in
Scientific American.
ANYWAY, about halfway into the novel (Chapter 20: "Into the M-Set"),
a quote from Albert Einstein appears. I'd like to reproduce it here:
The most beautiful thing we can experience is the mysterious. It is the source of
all true art and science. He to whom this emotion is a stranger, who can no
longer pause to wonder and stand wrapt in awe, is as good as dead.
Who could disagree with that?
CONCLUSION
In this page we've looked at the the simplest fractal - the Cantor set - and
the Mandelbrot set, which has been called "the most complicated object in
mathematics" by John H. Hubbard, an authority on the set. Both sets are
fascinating and charming in their own ways.
There's a lot of self-similarity in the Mandelbrot set - but you never see
exactly the same thing twice. It's absolutely full of surprises!
If you've taken some time to have a look through the above pages, by now
you've probably gained a reasonable grasp of what the M-set is all about,
and perhaps picked up a few techniques for exploring and representing it
yourself.
However, we've only scratched the surface. There are other ways of
representing the M-set which look quite different from the somewhat
"traditional" way discussed here; and they are no less valid. If you hunt
around on the web, no doubt you'll find some of them. So now, it's up to
you! Why don't you continue your journey?
UPDATE, Wednesday, 6th October 2010
Just yesterday, I discovered a series of six YouTube videos which together
make up a production called "Fractals: the Colors of Infinity". This
remarkable program discusses, in considerable detail, fractals in general
and the Mandelbrot Set in particular. The host is Arthur C. Clarke, and the
program begins with a reference to Albert Einstein's "... most beautiful
thing..." comment (see above).
In this program, there are many sequences showing the M-set in all its
glory, in full and fizzing colour, along with clear explanations and some
speculative thought about what it all means. The soundtrack features the
music of Pink Floyd's
David Gilmour
(click
here
to visit Mr. Gilmour's website). I recommend it highly. Here is the URL
for the first of these six videos:
http://www.youtube.com/watch?v=qB8m85p7GsU
Videos 2 to 6 are then easily found within YouTube's own indexing system -
along with many other videos in similar vein. So, what are you waiting for?
Go ahead - enjoy them!
UPDATE, Saturday, 30th October 2010
I've just become aware that Benôit Mandelbrot died on Thursday 14th
October - just 16 days ago - at the age of 85.
Of course I'm saddened; but I'd like to say that I can't help but have my
spirits lifted by what this "father of fractal geometry" has achieved.
Since his discovery of the M-set in 1980, his contribution has helped
enormously to give mathematics a more human face, not least by drawing
attention to the fact that nature itself appears to be fractal.
(Click
here
to read the Wikipedia article, and
here
for the New York Times obituary.)
R.I.P., Dr. Mandelbrot. The world is a better, more thoughtful place for
your having been here.
My home page
Preliminaries (Copyright, Safety)
Fractals #1: the Cantor and Mandelbrot Sets




 But we can imagine what would happen.
"Eventually", there will be no line segments left at all; there will just be
a dust of isolated points.
But we can imagine what would happen.
"Eventually", there will be no line segments left at all; there will just be
a dust of isolated points.


And little fleas have lesser fleas, and so on ad infinitum.
And the great fleas themselves, in turn, have greater fleas to grow on,
While these again have greater still, and greater still, and so on.




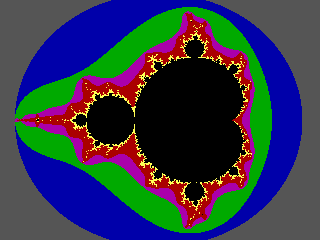
(the whole set)



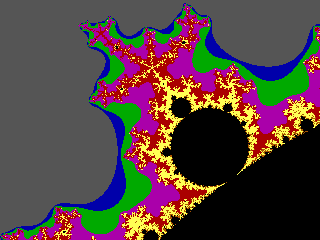


("Winter in Mand-land" - my favourite bit of the M-set)

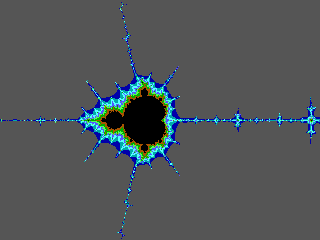

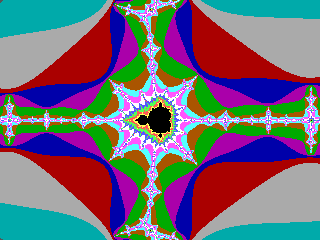





(invaded by "South Park"'s Mr. Hanky??!)


(here's lookin' at you, kid)














(trying to survive in an algal bloom?)




(a view from the east)

(more branches)


(still more branches)


(Andrew laMance's "Love Canal")


"The Utter West"

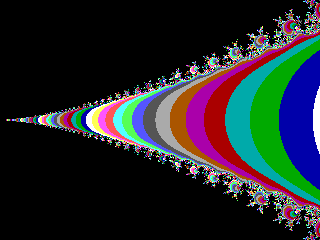
"The Last Trump"...?







 Return to Computer Graphics sub-menu
Return to Computer Graphics sub-menu

