
FURTHER QUATERNION STUFF
(and a brief look at other number systems with even more dimensions)
Page 1
of this set of three web-pages presented a background to the real number
system that we all learned in school, and then progressed to some of the
basic properties of complex numbers. The fact that both real and complex
numbers form fields was mentioned, along with the fact that the
multiplication of complex numbers can be seen to have a natural connection
with rotation in the Argand plane.
Page 2
recounted the story of the discovery, in 1843, of the quaternions by Sir
William Rowan
Hamilton
- and then went on to give a reasonably in-depth discussion of the basics
how they "work", with particular emphasis on the fact that multiplication is
not commutative, so that they form a (strictly) skew field. (I also growled
about how I think that the over-formal way in which mathematics and science
are often presented has caused a lot of damage from an educational point of
view.
The application of quaternions to computer animation was mentioned, along
with the fairly recent suggestion that restoring the original quaternionic
nature of Maxwell's electromagnetism equations may well have some extremely
significant consequences for technology (and a whole lot more besides). In
this connection, the concept of vectors was mentioned very briefly.
Along the way, the surprising fact that (in quaternion terms) negative real
numbers have infinitely many square roots was raised. Hamilton's
letter
to his friend John T. Graves was mentioned in this connection.
In this, the third page, I'll develop the matter of square roots further
(just because it is so intriguing, basically!), and briefly introduce
the last of the four "normed division algebras" (the octonions), and
also something called the biquaternions!
SQUARE ROOTS
Toward the end of Hamilton's letter to John Graves (mentioned above), he
gives a formula involving a square root. It's not clear (at least, not to
me) how he obtained this; but at some point I decided to try to work out,
from first principles, my own general expression for the square root of a
quaternion - and that formula appeared in my result.
I'll give my working shortly; but first, by way of motivation (and I'm sure
that by now you know that I'm big on motivation), let's look at the simpler
problem of finding a general formula for the square root of a complex
number.
SQUARE ROOT OF A COMPLEX NUMBER
The aim of the following exercise is to find a general formula for the
square root of the general complex number, x + yi , where x and y are both
real.
Note: we can always put a complex number into its polar form (see
page 2),
and find its "principal" square root by taking the square root of its
modulus and halving its argument; but here, we'll concentrate on doing it
algebraically.
Suppose that p + qi , where p and q are also both real, is such a square
root. Then
(p + qi)2 = x + yi
, therefore
p2 + 2pqi -
q2 = x + yi
Equating real coefficients and imaginary coefficients, we obtain
p2 -
q2 =
x and 2pq = y
From the second of these, we obtain q = y/2p . Substituting this into the
first:
p2 -
y2/4p2
= x , therefore 4p4 -
4p2x -
y2 = 0
This can be considered as a quadratic equation in
p2. Quartic equations of this type, in
which linear and cubic terms are absent, are sometimes called
biquadratic. It's possible to solve them by using the quadratic
formula as a first step, as follows:
p2 = [4x ±
sqrt(16x2 +
16y2)]/8 =
[x ± sqrt(x2 +
y2)]/2
Note that we are using "sqrt" as an abbreviation for "square root of".
Now, since we are insisting that p must be real, and since [x -
sqrt(x2 +
y2)] must be negative (unless y = 0, in
which case the value of this expression will also be 0), we can simply drop
the "-" from the "±". Then, taking square roots:
p = ±sqrt[x + sqrt(x2 +
y2)] / sqrt(2) or p =
±sqrt[sqrt(x2 +
y2) + x] / sqrt(2)
Next, substitute this into q = y/2p :
q = y × sqrt(2) / {±2 × sqrt[sqrt(x2 +
y2) + x]}
= ±y / {sqrt[sqrt(x2 +
y2) + x] × sqrt(2)}
Multiplying both the top and bottom of this fraction by
sqrt[sqrt(x2 +
y2) - x] :
q = ±y × sqrt[sqrt(x2 +
y2) - x] /
{sqrt[x2 +
y2 -
x2] × sqrt(2)}
= ±y × sqrt[sqrt(x2 +
y2) - x] /
{sqrt[y2] × sqrt(2)}
= ±y × sqrt[sqrt(x2 +
y2) - x] /
{y × sqrt(2)}
STOP RIGHT THERE!
That last step is not quite correct. Can you see why?
When we take the square root of y2,
it's reasonable to expect that the answer will be y. What else would it be?
When we talk about the "square root" of a (positive) number, it's understood
that we're referring to the positive square root. For example, the
"square root of 49" is 7, rather than -7 (even though they are both square
roots of 49, since the square of each is 49).
If we were to use this process in a particular case with actual numbers for
the coefficients, there'd be no confusion. However, when we use algebraic
symbols (pronumerals) to stand for coefficients in fully-general formulas,
as in our case here, we have to be careful.
In the development of our square root formula, y could be positive or
negative (or zero). If it's negative, we need to be aware that the
positive square root of y2 is
-y, not y.
To cut a long story as short as possible, and basically to "make things
work", what we can do here is put y in the denominator - as we've done - but
then also multiply the entire term by the "signum function", sgn(y). This
takes the value 1 if y is
positive, -1 if it's negative,
and 0 if it's zero.
This fixes everything so that the formula will give us correct answers, no
matter what the value of y is.
Okay - let's rewrite that last line with the corrrection, and continue:
... = ±y × sqrt[sqrt(x2 +
y2) - x] /
{y × sqrt(2)} × sgn(y)
therefore q =
±sqrt[sqrt(x2 +
y2) - x] / sqrt(2) × sgn(y)
So, finally, the two square roots of x + yi are
±{sqrt[sqrt(x2 +
y2) + x] +
sqrt[sqrt(x2 +
y2) - x]×sgn(y) i} / sqrt(2)
Well, it's a bit tedious getting there; but the final formula itself isn't
really all that complicated - and it does work! For example, it gives the
square roots of 3 + 4i as ±(2 + i) . [You can check this by calculating
(2 + i)2.] Also, significantly, it
gives the square roots of 3 - 4i as ±(2 - i), rather than as ±(2 + i), which
it would give if we didn't include the sgn(y) in the expression!
Make up some examples of your own: choose some complex number, square it,
and then use this formula to find the square roots of the result. You'll
find that it always gives correct answers.
Note that the two square roots of any complex number are opposite each
other with respect to zero in the Argand plane, corresponding to an
anticlockwise rotation of 180 degrees as a result of multiplying by -1 , or,
indeed, to a clockwise rotation of 180 degrees as a result of dividing by
-1 (take your pick!). Thus, following the examples just given, the two
square roots of 3 + 4i , i.e. 2 + i and -2 - i , are located 180 degrees
apart, on opposite sides of the origin; similarly for the two square roots
of 3 - 4i , i.e. 2 - i and -2 + i .
SQUARE ROOT OF A QUATERNION
Following the same basic idea as for finding the square root of a complex
number (above), let's now attempt to produce a formula for the square root
of the general quaternion, w + xi + yj + zk , where w, x, y, and z are all
real numbers.
Suppose that p + qi + rj + sk is such a square root (with p, q, r, and s all
real numbers); then
(p + qi + rj + sk)2 = w + xi + yj + zk
We have no choice but to multiply the left-hand side out. (Sorry!)
p2 + pqi + prj + psk +
pqi - q2 + qrk - qsj +
prj - qrk - r2 + rsi +
psk + qsj - rsi - s2
= p2 -
q2 -
r2 -
s2 + 2pqi + 2prj + 2psk
Well, it could be worse. So:
p2 -
q2 -
r2 -
s2 + 2pqi + 2prj + 2psk
= w + xi + yj + zk
Equating coefficients:
p2 -
q2 -
r2 -
s2 =
w
2pq = x
2pr = y
2ps = z
The last three of these give
q = x/2p
r = y/2q
s = z/2p
which we can substitute into the first one:
p2 -
x2/4p2 -
y2/4p2 -
z2/4p2 = w
, therefore
4p4 -
(x2 +
y2 +
z2) =
4wp2
or
4p4 -
4wp2 -
(x2 +
y2 +
z2) = 0
(Note the similarity of this biquadratic equation to the corresponding
equation in the complex case, above.)
Treating this as a quadratic equation in
p2 , and applying the quadratic
formula:
p2 =
{4w ± sqrt[16w2 + 16(x2 +
y2 +
z2)]} / 8
= {w ± sqrt[w2 +
x2 +
y2 +
z2]} / 2
Now, since we are insisting that p be real, and since
{w - sqrt[w2 +
x2 +
y2 +
z2]} must be negative (unless x, y, and
z are all 0, in which case the value of this expression will also be 0), we
can simply drop the "-" from the "±". Then, taking square roots:
p = ±sqrt{w + sqrt[w2 +
x2 +
y2 +
z2]} / sqrt(2)
To make life a bit easier, let's refer to
sqrt{w + sqrt[w2 +
x2 +
y2 +
z2]} as N, to save having to keep
spelling it out. Then:
p = ±N / sqrt(2)
Now substitute this into q = x/2p :
q = x / [2 × ±N / sqrt(2)] = ±x / [N × sqrt(2)]
Similar substitutions into r
= y/2p and s =
z/2p yield, respectively:
r = ±y / [N × sqrt(2)] and
s = ±z / [N × sqrt(2)]
Thus, finally, the square roots of
w + xi + yj + zk can be written as:
±[N + (x / N) i + (y / N) j + (z / N) k] / sqrt(2)
where N = sqrt{w + sqrt[w2 +
x2 +
y2 +
z2]}
WHEW!
So, at last, we have our formula. Now, let's look at its implications.
Firstly, if one or more of x, y, and z is not equal to zero, then - whatever
value w takes - N will be positive and the formula works fine. (If just
one of x, y, and z is not equal to zero, then effectively we're just
taking the square root of a complex number, and the formula essentially
reduces to that for the complex case given above.)
Secondly, if all three of x, y, and z are equal to zero, then N = sqrt(2w)
if w is positive [in which case the square root is just sqrt(w), as we'd
expect]; and zero if w is zero or negative. Since the formula involves
division by N, and we can't divide by zero, we need to look at these last
two cases more carefully:
On the one hand, if w, x, y, and z are all equal to zero, then the whole
quaternion is just zero, and so is its square root - without having to
resort to using the formula at all.
On the other hand, if w is negative, and x, y, and z are all zero, things
get a lot more interesting. Again, N is zero (can you see why?), so that,
again, we can't divide by it. Thus we need to adopt another approach.
Suppose (p + qi + rj + sk)2 =
-M2 , where p, q, r, s, and M (for
modulus) are all real numbers (so that
-M2 is the negative real number w).
Then:
p2 -
q2 -
r2 -
s2 + 2pqi + 2prj + 2psk =
-M2
Since we've set this up so that the right-hand side (i.e.
-M2) is a real number, the left-hand
side must also be a real number. This means that
2pqi + 2prj + 2psk = 0 , therefore 2p(qi + rj + sk) =
0
This means that either p = 0 , or all three of q, r, and s are equal to 0 .
If q = r = s = 0 , then p2 =
-M2 . However, since p is real, this is
impossible unless p is zero (as squares of non-zero real numbers are always
positive, and -M2 is negative unless M
is zero.)
Hence p must be 0 . This means that
-q2 -
r2 -
s2 =
-M2 , therefore
q2 +
r2 +
s2 =
M2
- which means that (q,r,s) is any point on the surface of a sphere of radius
M, centred on the origin, in a three-dimensional space in which the three
axes represent, respectively, imaginary quaternion parts.
Thus we have now proved that, in quaternion terms, there are infinitely many
square roots of any negative real number, which are all purely imaginary and
equidistant from the origin; and, also, that negative real numbers are the
only quaternions that have this property.
The amazing thing is that we can achieve this result by using little more
than high-school level algebra (referred to by mathematicians as "elementary
algebra")!
By the way: interestingly, the quaternion square root formula just presented
doesn't have the problem mentioned earlier with respect to the corresponding
formula for complex numbers. In the latter, it was necessary to multiply one
term by the signum function to ensure a correct answer every time;
but this isn't necessary with the former, in which the problem "takes care
of itself". In that sense, somewhat surprisingly, the quaternion formula is
more "robust" than its complex counterpart.
Recall that all this started with one man's attempt to generalize the
rotational nature of complex number multiplication to three dimensions.
He certainly succeeded: each of the three imaginaries represents a
rotational degree of freedom. The fact that it was necessary to go to
four dimensions to achieve the result, and also the astonishing
result about infinitely many square roots of negative real numbers, add an
element of intrigue to the proceedings.
In addition, there's an irony about all this that appeals to me.
It's common to think, is it not, that our three-dimensional world is
reality, and that dreamy ideas about a fourth dimension involve using
our imagination. Yet the three "imaginary" quaternion dimensions
correspond in a natural way to our "real" world, with the "real" quaternion
dimension corresponding to the "imaginary" one!
Actually, it's this kind of consideration which lies at the heart of the
"problem" with quaternions. When Gibbs and Heaviside simplified Maxwell's
electromagnetism equations, they did so by effectively separating the real
(scalar) components from the imaginary (vector) components.
This led to the development of scalars and vectors as two quite distinct
concepts.
I'll admit that, as a student, I always had trouble with the vector concept.
I always had the feeling that there was something missing - that, somehow,
we weren't being told the full story. Why were there two distinct
kinds of product involving vectors (the scalar or "dot" product, and
the vector or "cross" product), which were quite different and
appeared to have nothing whatever to do with each other? Why was the
dot product a scalar, and - even more confusing - why was the cross
product a vector at right-angles to both of the vectors being
multiplied; and furthermore: why, when the order of multiplication
was reversed, did the resulting vector point in the opposite direction?
Why should the universe have this asymmetry built into it?
I feel that an understanding of quaternion algebra goes at least part of the
way to addressing these questions. It's almost as if the nature of the
vector dot and cross products follows as a necessity: "How could it be any
other way?".
FOR THE RECORD
Quaternions came before vectors. Indeed, it was Hamilton himself who
originally coined the terms "scalar" and "vector", to describe the real and
imaginary parts, respectively, of quaternions. It was only later that these
concepts took on a life of their own, without reference to the quaternions
that gave rise to them in the first place. I find it outrageous that
students of the physical sciences are now usually taught only half of
the full story; and I raise the issue of how many vested interests have been
only too happy to maintain the deception; and again, I ask why...
(I'm not alone in my concerns. See
this page
to read an article by a kindred spirit. Also, click on the links and have a
good look around the site - most interesting...)
WE NEED TO STAND UP FOR TRUTH AND HONESTY IN SCIENCE, COME WHAT MAY.
There's more, however. The quaternions are only one of several types of
hypercomplex numbers. Have a look at
this page
in which some of these are listed, with links leading to more detail.
Don't worry if you don't understand all the terminology (I don't understand
a lot of it myself!); just have a look over the page to get an idea of the
scale of the subject.
Two of these various types of algebras are the biquaternions and the
octonions, which are both extensions of the quaternions - much as the
quaternions are themselves an extension of the complex numbers, which are in
turn an extension of the real numbers...
The biquaternions are somewhat like the quaternions; but instead of allowing
only real coefficients, we now allow complex coefficients!
This doubles the number of dimensions from four to eight.
The octonions are something else again! With this algebra (also
eight-dimensional), we lose not only the Commutative Law of Multiplication
(CLM), but also the Associative Law of Multiplication (ALM). This is a major
alteration, having a far more profound impact than the loss of the CLM.
However, like the real and complex numbers and the quaternions, the
octonions still form a normed division algebra - which basically
means that, in spite of the extra "damage" inflicted by the loss of the ALM,
a kind of division is still possible and makes some sort of reasonable
sense. The octonions are the fourth - and last - such division algebra; even
the biquaternions don't measure up in this regard.
These - and many even more peculiar structures - were investigated in the
19th century, after Hamilton started the ball rolling by introducing the
quaternions. One of the main researchers was William Kingdon
Clifford,
after whom the "Clifford algebras" (which have even more dimensions!)
are named.
The octonions were discovered by John T. Graves (to whom Hamilton wrote his
famous letter - see above). To learn more, click on
this link
which leads to a paper by John Baez (a photograph of whom, with some
friends by Dublin's Broome Bridge admiring the plaque to Hamilton, can be
accessed via a link in
page 2
of this article). Also, may I recommend a visit to
John Baez's home-page,
in which you will find plenty of links to thought-provoking stuff, not all
of it mathematical. (In particular, may I recommend
this article.)
UPDATE, Saturday, 21st April 2007
On this page:
http://www.math.oregonstate.edu/bridge/papers/
you will find links to a number of articles by
Tevian Dray,
a Professor of Mathematics (and one of those four visitors to the Broome
Bridge), and his colleague
Corinne A. Manogue,
a Professor of Physics (both at Oregon State University), who have tackled
the issue of how vectors in general - and vector calculus in particular -
are often taught in a less-than-intuitive way, which makes it hard for
students to grasp the concepts, as well as being less than totally helpful
for scientists, who prefer a more obviously practical, "applied" approach
than the traditional abstract, "pure" mathematical approach.
The penultimate one of these links is to a .pdf file entitled "The Geometry
of the Dot and Cross Products", which addresses the issues I raised above.
Well worth a look! I'm quite sure that had I seen something like this as a
student, I'd have been able to latch on to the essential ideas much more
quickly and easily.
(By the way: in addition to their shared interest in how mathematics is
taught, and how it is used by physicists, Professors Dray and Manogue have a
common research interest in the octonions and their possible applications.)
I'll just squeeze in one more link about the development of algebraic
systems.
This excellent page
gives a history of hypercomplex numbers from the seventh century up to the
present, and covers in summary form just about everything I've said in these
three pages about the development of the subject. It's easy to read, and
gives a good, clear perspective. Highly recommended.
(I actually included that link about halfway down
page 1
of this article, with reference to the origin of the mathematical use of
the term "imaginary"; but now, having read
page 2
and this page also, you may
find that you can get a lot more out of it than previously.)
CONCLUSION
Well! This article on quaternions, like Topsy, "just growed" - to three
pages.
I hope you've managed to get something out of it. As I'm sure you've
realized by now, I hope that the whole world latches on to the very
practical issues the subject raises, and sooner rather than later: an
application of this theory to the production of cheap energy, consigning the
oil industry to history as soon as possible - thus enabling a serious
attempt to be made to scale back greenhouse gas production, and removing the
perceived need for greedy rich nations to inflict their particular kind of
barbarism on less powerful nations which just happen to have large oil
deposits.
If abstract algebra can help make the heartfelt sentiment expressed by the
slogan
"NO BLOOD FOR OIL"
actually come to pass, and also pull the rug out from under the resurgent
nuclear power lobby at the same time, I'll be cheering. If you've caught my
drift, and are inspired to help spread the word and draw attention to these
matters, I'll be cheering even louder.
(If you don't have the foggiest notion what I'm talking about, please visit
my
Zero-point energy
page to find out.)
Over to you!
Return to
Quaternions - page 1
Return to
Quaternions - page 2
My home page
Preliminaries (Copyright, Safety)
Quaternions: an old (and new) look at four dimensions - page 3
 )
)
 -
and maybe raise a bit of hell about a few other things too, while we're at
it.
-
and maybe raise a bit of hell about a few other things too, while we're at
it.


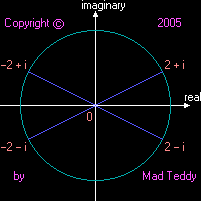

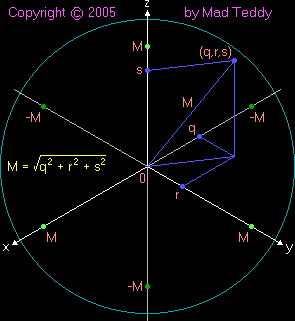 (Recall this diagram from
page 2.)
(Recall this diagram from
page 2.)





 Return to Mathematical stuff menu
Return to Mathematical stuff menu

