
INTRODUCTION
Of all the mathematical topics discussed in this website, this one probably
at least appears to be the most technical.
The reason for including it at all is that I believe quaternions may be set
to make something of a "comeback". The concept was first mooted in the early
19th century; it enjoyed some popularity for a few decades, and was then all
but forgotten late in the 19th century, and for most of the 20th.
It has resurfaced in recent years because of the fact that it has found a
significant rôle in three-dimensional computer graphics programming, helping
greatly to solve some very practical problems. However, as I've just hinted,
there is more to be said about it. My aim is to give a fairly simple
introduction here - so that, if the idea is new to you, and if you run
across it somewhere else, you won't be totally at a loss to know what it's
all about.
This article has grown to the point where I've found it convenient to break
it up into three pages. In this, the first page, I give an overview of the
development of number systems up to and including complex numbers. At the
end, you will find a link to the second page, which introduces the
quaternions themselves. The third page develops a fundamental aspect of the
concept, and also presents a very brief introduction to other number systems
with even more dimensions.
Let's start by thinking about how children develop mathematical ideas.
To a newborn baby, there is only one number: NUMBER ONE.
"Feed ME! Burp ME! Change ME! Put ME to sleep!"
Hopefully they grow out of that fairly quickly. As they learn to talk and
think a bit, at some point they will realize that they have several
funny-shaped, quite useful little things on the ends of their arms - ten of
them, to be precise - and, with a bit of luck, they'll develop an interest
in counting, probably using their fingers as an aid.
Thus begins their foray into the world of numbers. I believe that natural
curiosity allows children to view numbers as just another toy, and think of
them as fun. (Sadly, this changes for so many when they start school.)
Interestingly, the numeral for "ten" consists of two characters: a "one"
and a "zero". The zero is something new. Kids start counting at 1, not 0.
This strange symbol stands, in some mysterious way, for "nothing", or
"something that doesn't exist" (other than the fact that we have to mention
it at all).
Zero develops a life of its own a bit later; for the moment, it's a
"filler", occupying a spot as a place value to show where something
else isn't.
I seem to remember that I felt some satisfaction when I first managed to
count to 100. One day, I made a point of counting out loud to 1000, and
drove everyone in the house nuts for a few minutes while doing so.
("Peculiar child!")
So, the first numbers kids learn about comprise what is known as the "set of
natural numbers" or the "set of positive integers". These numbers start at
1, and go on forever...
In primary school, most of a child's mathematical life is taken up with
learning to manipulate the natural numbers. The subject may be called
"arithmetic", or (less formally) "sums". (This is where many children switch
off; unfortunately, some never recover.)
Addition is the simplest operation. Subtraction comes next; this is where
zero reappears as an important entity in its own right, as the result of
subtracting a number from itself. (At this stage we don't try to subtract
a number from another number smaller than itself.)
Multiplication may be introduced as "repeated addition". "Two threes" may be
represented as six dots laid out in a two-by-three rectangular grid; until
they've learned their multiplication tables, kids can get the answers by
just counting the dots.
Division is a strange beast, and definitely more difficult than any of the
other three operations. This time, more often than not, things don't "work
out exactly", and in addition to the "answer" (i.e. the quotient), we often
get a mysterious extra bit called a "remainder".
"Long multiplication" is something of a quantum leap. Not only do you have
to know your multiplication tables, but you have to add columns of figures
as well.
"Long division", unfortunately, may remain a complete mystery for
many.
Bear with me, please - this is leading somewhere.
The next two hurdles are fractions and negative numbers.
I first ran across fractions in late primary school. Many kids struggled;
even nerdy old Teddy had a bit of trouble with them - initially, at least.
Negative numbers came along in early high school. They occurred as a result
of subtracting a number from a smaller number, and could be used to
represent debt. They could be thought of as "directed numbers", marching in
the opposite direction (left) to what now became known as positive numbers
(which marched to the right). For the first time, the idea of a "number
line", with zero in the "middle", was introduced, thus giving a geometrical
perspective.
The representation of the absolute value of the difference of two
numbers as the distance between them could be introduced. In
topological terms (see my page about
topology
to read more), this brings in a metric concept to complement the
algebraic nature of arithmetic. (I'll return to this meaning of the
word "algebra" in the following page.)
Also in early high school, decimals were introduced. Fractions could be
represented as strings of digits occupying place value positions to the
right of the units, and separated from them by a dot. It turned out that the
decimal representation of a fraction was always either a terminating
decimal or a repeating decimal. (Note that it's actually possible to
think of a terminating decimal as a repeating decimal, with infinitely many
zeros after the final "significant figure".)
The idea of a square root was introduced. It turned out that positive
numbers had square roots, and so did zero (which is its own square root) -
but that negative numbers didn't. This was because "plus times plus is plus"
and "minus times minus is (also) plus" (another of life's mysteries, to many
people!).
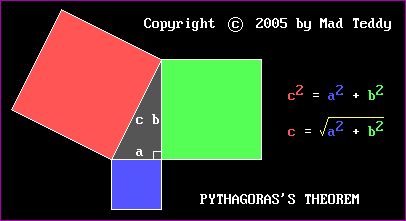
The most obvious use for square roots was in Pythagoras's Theorem:
Armed with this, one could calculate lengths of fencing required to
subdivide land into plots of various shapes, etc. (something which has been
done successfully since ancient times). Students learned that, usually,
square roots were irrational; that is, they couldn't be expressed as
either a terminating or a repeating decimal.
With geometry becoming an increasingly important part of the picture, it was
only a matter of time before the length of the circumference of a circle was
considered. A strange number called "pi" came into the proceedings; for any
circle, the length of the circumference was equal to this number times the
length of the diameter. Pi was initially introduced as being equal to 22/7 -
later better approximated as 3.1416.
It was quite a surprise to find that the true value of pi, in decimal terms,
went on forever without repeating. So the "fractional part" wasn't a
fraction at all! Just like the square roots of most numbers, Pi was
irrational.
An even bigger surprise was that pi was a different kind of
irrational number. Square roots (and cube roots, etc.) were surds;
whereas pi was transcendental!
OMMM...
So, finally, we had been formally introduced to the
set of real numbers.
Cartesian geometry (pioneered by
René Descartes
)
showed how we could have two number lines, one horizontal (the "x-axis") and
one vertical (the "y-axis"); we could represent each point on the resulting
plane by an ordered pair of real numbers - and we could plot graphs,
showing the relationship between x and y in an equation involving both.
Simple equations involving only one variable and no squares or higher powers
had been introduced at some point, and we had learned techniques for solving
them. Since the Cartesian graphs of such equations in two variables
are always straight lines, the word linear is now used for such
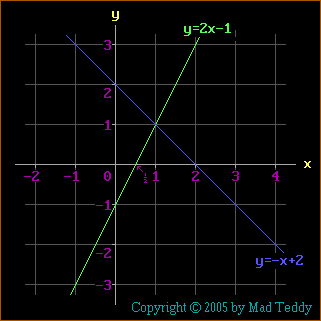
equations in any number of variables. Here are two examples of graphs
of linear equations in two variables (x and y):
When we have equations of the form shown, i.e. "y = (some linear expression
involving x)", if we allow y to equal zero, we obtain a linear equation in
just one variable (i.e. x). The point where the line graph of the
two-variable version crosses the x-axis is the solution of the
single-variable version. Thus, the equation y = -x+2 becomes -x+2 = 0, the
solution of which is x=2; and the equation y = 2x-1 becomes 2x-1 = 0, the
solution of which is x=½.
Since the graph of any linear equation involving both x and y is a sloping
line, which must cross the x-axis at just one point, it's clear that the
corresponding equation involving only x has exactly one solution. (This has
to do with what mathematicians call the "intermediate-value theorem".)
Then quadratic equations came along - and this, finally, was where things
started to become really interesting. Having learned to solve "simple"
quadratic equations by factorizing, the technique of "completing the square"
was introduced to deal with equations where factorization "didn't work", and
was ultimately utilized to produce the "quadratic formula":
If ax2+bx+c = 0 , then x =
[-b ± square root of (b2-4ac)] / 2a
(The symbol "±" means "plus or minus"; thus it gives us a shorthand way of
representing two numbers.)
Now, as mentioned, it had been made clear that "negative numbers don't have
square roots". But here we had a formula in which, apparently, negative
numbers could have square roots (if
b2 happened to be less than 4ac). What
were we to make of all that?
We can at least begin to investigate this matter by using Cartesian
geometry.
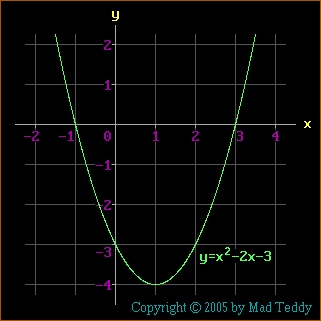
Consider the equation x2-2x-3 = 0 .
The left-hand side can be factorized; then the equation becomes (x-3)(x+1) =
0 . There are two possible solutions, each obtained by setting one of the
factors equal to zero - so that x is equal to 3 or -1 .
Suppose we draw the graph of the equation y =
x2-2x-3 , or y = (x-3)(x+1) :
Graphs of quadratic equations of this form are always U-shaped curves called
parabolas. If the number multiplying
x2 is positive, the parabola opens
upwards; if it's negative, the parabola opens downwards. (In this case, that
number is 1, which is positive - so the parabola opens upwards.)
From this graph, it can immediately be seen that the curve cuts the x-axis
in two points, at -1 and 3, i.e. at the two values which are the solutions
of the original equation.
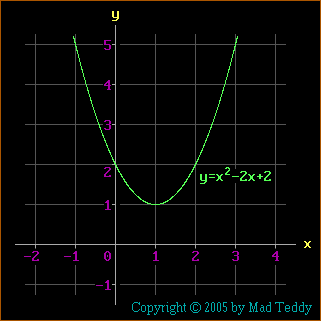
Now consider another quadratic equation:
x2-2x+2 = 0 . (The expression on the
left-hand side is obtained by adding 5 to the expression in the previous
example.)
This time, factorizaton isn't possible; so, to solve the equation, we resort
to using the quadratic formula. With a=1, b=-2, and c=2, we obtain the
following:
x = [2 ± (square root of -4)] / 2 = 1 ± (square root of -1)
(To obtain this final result, we assume that it's okay to extend the rules
which apply to square roots of multiples of positive numbers, to square
roots of multiples of any real numbers.)
So we have to deal with this "square root of -1". Mathematicians normally
represent it by i. Thus the solutions of the equation are 1±i, i.e. 1+i and
1-i.
Okay - let's have a look at the graph of
y = x2-2x+2 , and see if it throws any
light on this matter:
This time, the parabola doesn't intersect the x-axis at all! Thus, the graph
tells us that there are no real solutions to
x2-2x+2 = 0 , though without giving
much help in deciding whether there may be solutions that are in some way
"unreal".
How teachers of mathematics at various levels deal with this may be
determined by the subject's syllabus; in some cases, the teacher may be able
to choose to tell students either that such an equation has no
solutions, or that is has two unreal solutions.
In my own experience as a student, simple references to unreal solutions
were made at high school and in a first maths course at matriculation
college; this was adequate for our needs at the time. In a second, more
advanced matric. maths subject, and again at university, the issue was
tackled formally in a systematic way.
The idea of an "unreal" number is a convenient way to introduce students to
the concept of a number other than real in an informal way. However, it soon
becomes necessary to distinguish three types of number: purely real,
purely "unreal", and partly both. For historical reasons, purely "unreal"
numbers are formally known as "imaginary" numbers (the simplest of which is
i itself); and numbers like 1+i, which are partly real and partly imaginary,
are known formally as "complex" numbers.
Both terms - "imaginary" and "complex" - are unfortunate. They seem to imply
that there is something difficult about dealing with them. (It was Descartes
who
introduced
the term "imaginary".) Initially, they take a bit of getting
used to; but once you're comfortable with them, they are an extremely
powerful tool in some areas - notably, in AC circuit theory. Deft use of
complex numbers can reduce the analysis of a complicated circuit to quite an
easy exercise.
This web-page
provides a simple introduction to complex numbers, including some
historical background.
The issue of square roots of negative numbers was seriously addressed by
Italian mathematicians in the 16th century. At the time, the quadratic
formula was known, and attempts were being made to find corresponding
general formula solutions to cubic (third-degree) and quartic
(fourth-degree) equations. These attempts were successful. To read more
about these matters, and to get a more comprehensive idea of the history of
complex numbers, visit the following web-pages which give details of some of
the main players:
Tartaglia,
Cardano, and
Ferrari.
Like the quadratic formula, the solutions to both cubic and quartic
equations depended heavily on the ability to deal with square roots of
negative numbers. It should be remembered that, at that stage, even negative
numbers were still viewed by some mathematicians with suspicion, so that
complex numbers must have caused even more consternation.
It seems to me quite remarkable that such successes occurred, given the
limited understanding of these important underlying matters at the time; but
then, that's probably how major advances in mathematics have always been
made. (The same is true for science.) A certain amount of intellectual
courage is called for.
The history of mathematics and science is fascinating. If you read
your average maths or science textbook, you could be forgiven for thinking
that the various disciplines have developed in an orderly, neat and tidy
fashion - whereas, in many instances, nothing could be further from the
truth.
Against a background of frequent wars, political instability, and poverty,
there are all too often the fiery tempers, bad attitudes, and sundry other
personality defects of the major players themselves. All in all, it's quite
astonishing that any real progress is ever made; but - perhaps
because of these challenging factors, rather than in spite of
them - significant advances do occur nonetheless!
Having now established a foundation for complex numbers, let's have a brief
look at arithmetic involving them.
Addition: easy; just add the real parts and the imaginary parts separately.
For example: (7+3i) + (2+i) = 9+4i .
Subtraction: no more difficult; again, deal with the real and imaginary
parts separately. For example: (-6+2i) - (4-5i) = -10+7i .
Multiplication: use a technique similar to binomial expansion as in the
algebra of real numbers, but remember that
i2=-1 . For example: (2+3i) × (5-2i) =
10-4i+15i-6i2 = 10+11i-(6×-1) =
16+11i .
An interesting and important special case of multiplication occurs when we
multiply a complex number by its complex conjugate (the same number
but with the sign of its imaginary part changed): (a+bi) × (a-bi) =
a2-abi+abi-(-b2)
=a2+b2 .
The result is a purely real number, as the imaginary parts cancel each
other to zero.
Division: the most complicated of the four basic arithmetic operations, but
still not really all that difficult. The trick is to make sure that any
fractions that result have real denominators; so we simply multiply both the
dividend and the divisor by the divisor's complex conjugate. For example:
(2+i)/(3-i) = [(2+i)×(3+i)]/[(3-i)×(3+i)] = (5+5i)/10 = (1+i)/2 = ½+½i .
I'll return to complex numbers shortly; but first, we need to look at
certain rules regarding arithmetic.
Let's briefly revisit the real numbers. I recall that, in early high school,
our maths teacher made a point of listing what I seem to remember were
referred to as the "number laws":
1. Commutative law of addition (CLA): a+b = b+a . (The order in which
numbers are added makes no difference.)
2. Associative law of addition (ALA): (a+b)+c = a+(b+c) . (When adding a
list of numbers, you can start from either end.)
3. Commutative law of multiplication (CLM): a×b = b×a . (The order in which
numbers are multiplied makes no difference.)
4. Associative law of multiplication (ALM): (a×b)×c = a×(b×c) . (When
multiplying a list of numbers, you can start from either end.)
5. Law of addition of zero (LAZ): a+0 = 0+a = a . (Adding zero to a number
makes no difference.)
6. Law of multiplication by unity (LMU): a×1 = 1×a = a . (Multiplying a
number by 1 makes no difference.)
7. Law of opposites (LO): For any number a, there exists a unique number -a
such that a+(-a) = (-a)+a = 0 .
8. Law of reciprocals (LR): For any number a, other than zero, there exists
a unique number 1/a such that a×(1/a) = (1/a)×a = 1 .
9. Distributive law (DL): a×(b+c) = a×b + a×c . (Also known as the
"distributive principle of multiplication over addition", or DPMA.)
I remember wondering what all the fuss was about. Weren't the first eight
obvious? Didn't everybody know all that, without having to have it spelled
out? (The ninth one looked a bit confusing, but I thought: ho hum, just learn the silly thing. Also, I was a bit puzzled about the apparent
discrepancy between 7. and 8. - why couldn't you divide by zero? -
but I put the matter on hold indefinitely and just carried on...)
It was only years later, when at university, that I began to realize the
importance of these rules, mainly because there existed mathematical systems
in which one or more of them didn't apply.
The rules - with a couple of extra "closure" rules, basically saying that
when you add or multiply real numbers, you get real numbers as a result -
together essentially say that the set of real numbers under addition and
multiplication form what is known as a field.
Why am I taking the trouble to go through all this?
Two reasons: firstly, to point out that the complex numbers also form a
field; and secondly, to foreshadow the far more interesting fact that the
quaternions don't, quite.
On a personal note:
Some years ago I was teaching a basic mathematics course to adult students.
One lady was having difficulty solving simple equations. She was able to
solve (for example) x+2=5 all right, obtaining x=3; but 2+x=5 would cause
her trouble. A bit of digging on my part revealed the fact that she'd had an
unhappy experience at school when one maths teacher had taken a dislike to
her, so that she learned almost nothing from him. The result was that she
didn't have a clear understanding that x+2 and 2+x meant the same thing -
i.e. she wasn't aware of the CLA!
I was able to correct the problem for her, and she happily went on to pass
the subject quite comfortably. So there you are: the "number laws"
aren't necessarily obvious to everyone, and there is a valid
reason to teach them to schoolkids! An object lesson for me: if you're a
nerd, at least don't be an arrogant nerd.
Back to complex numbers.
Since the real numbers can be plotted on a line, it's reasonable to suggest
that the imaginary numbers can be also. Since the number 0 exists in both
sets, it's reasonable to at least investigate the implications of including
both such lines in the Cartesian plane.
Various mathematicians came up with the idea in the late 18th and early 19th
centuries; the resulting plane is now known as the Argand plane after French
mathematician Jean Robert
Argand
- even though he wasn't the first to think of it. (Click on the link and
follow other links within the page to read more - this is a classic example
of how mathematics has often developed in a less-than-tidy way.)
In the Argand plane, real numbers are represented along the horizontal axis
(the Cartesian plane's x-axis) and imaginary numbers along the vertical axis
(the y-axis). Thus the point (2,-1) represents 2-i; (-3,5) represents -3+5i;
(0,-7) represents -7i; and so on.
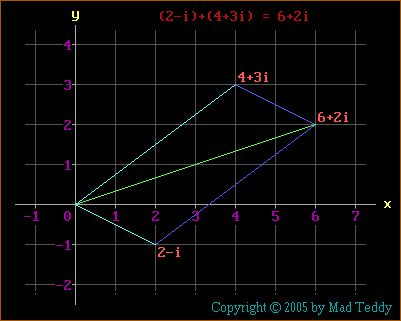
Addition in the Argand plane can be represented somewhat as a "parallelogram
of forces" is often represented in physics textbooks:
Subtraction is basically addition of the first number and the negative of
the second, so essentially it's the same from a graphical point of view.
With multiplication and division, things are more interesting. To see how
these work graphically, it's necessary to consider the polar form of
a complex number.
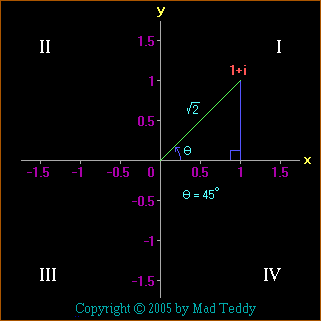
Let's start with a very simple complex number (is that a contradiction in
terms?
Note: the large white Roman numerals are just there to label the plane's
four quadrants. The reason for this will (I hope!) become clear
shortly.
Because the triangle's short sides are equal in length, i.e. the triangle is
isosceles, the two small angles are each 45 degrees. In particular,
the angle the hypotenuse makes with the real axis (at the origin) is 45
degrees. By Pythagoras's Theorem, the length of the hypotenuse is equal to
the square root of 2 (about 1.414).
The cosine of the angle made with the x-axis (45 degrees) is equal to the
horizontal side divided by the hypotenuse, i.e. 1/(square root of 2) .
The sine of that angle is equal to the vertical side divided by the
hypotenuse; this is also equal to 1/(square root of 2) .
The entire complex number can thus be represented as
(square root of 2) × (cos 45 degrees + i sin 45 degrees)
This is known as the polar form of the complex number. Instead of
focusing on the real and imaginary parts, we have now switched our attention
to the modulus, i.e. the distance of the complex number from the
origin (the square root of 2, in this case), and the argument, i.e.
the angle made with the real axis (45 degrees, in this case). This may be
abbreviated to
(square root of 2) × cis 45 degrees
where "cis" stands for "cos + i
sin" .
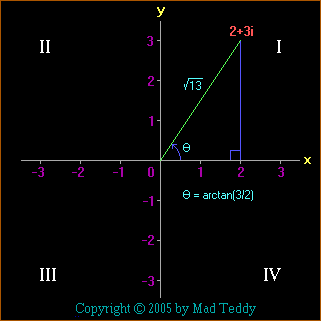
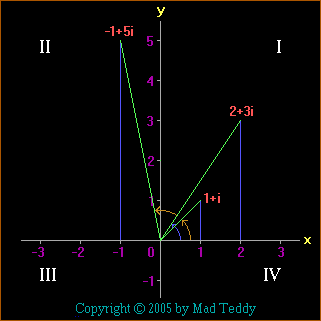
Now let's apply the same procedure to 2+3i .
This time, the modulus is equal to the square root of 13 (about 3.606) and
the argument is arctan(3/2), which is about 56.31 degrees.
Also, the cosine of the angle is 2/(square root of 13), and the sine of the
angle is 3/(square root of 13).
Thus 2+3i can be represented as
(square root of 13) × cis arctan(3/2) .
(Note that the last two diagrams are not to scale.)
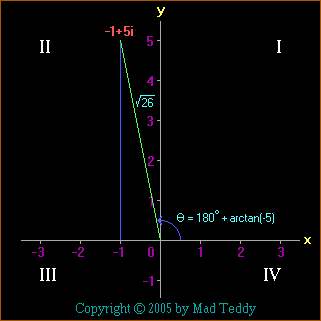
Next, let's multiply our two complex numbers together as described earlier:
(1+i) × (2+3i) = 2+3i+2i-3 = -1+5i
- and let's express this in polar form:
Modulus = square root of 26 (about 5.1); argument = 180 degrees+arctan(5/-1)
(about 101.31 degrees); the cosine of the angle is -1/(square root of 26);
the sine of the angle is 5/(square root of 26); and the number itself is
(square root of 26) × cis [180 degrees + arctan(-5)]
(Note: we always measure the argument anticlockwise from the
positive real axis; since the arctangent of a negative number is - by
definition - always between 0 degrees and -90 degrees, i.e. in the fourth
quadrant, IV, we
have to add 180 degrees in cases like this to make sure that we represent
the complex number where it should be, in the second quadrant,
II.)
Now, what do we observe?
Number: (1+i) × (2+3i) = -1+5i
The modulus of the product is equal to the product of the moduli of the
complex numbers being multiplied, as we might reasonably expect. However,
the argument of the product is equal to the sum of the arguments of
those numbers!
All together now
(to the same scale this time),
emphasizing how the angles add together (the brown arrows both represent
45-degree angles):
This is not a "one-off". It always works (click
here
to read more): when
multiplying complex numbers in polar form, we multiply their moduli
and add their arguments.
Similarly, when dividing, we divide the moduli and subtract
the arguments.
The point I'm trying to make here is that, with complex numbers,
multiplication is intimately linked to rotation. This fact is
perhaps the single most important feature which makes the field of complex
numbers such an important and practical tool in many situations.
Okay - that's enough background. On to quaternions!
Proceed to
Quaternions - page 2
Proceed to
Quaternions - page 3
My home page
Preliminaries (Copyright, Safety)
Quaternions: an old (and new) look at four dimensions












 ), 1+i . We plot this on the Argand plane,
join it to the origin (the point 0), and draw a line down from it to meet
the real axis (at 1). This gives us a right-angled triangle.
), 1+i . We plot this on the Argand plane,
join it to the origin (the point 0), and draw a line down from it to meet
the real axis (at 1). This gives us a right-angled triangle.
Modulus: 1.414 × 3.606 = 5.1
Argument: 45 + 56.31 = 101.31 (degrees)


 Return to Mathematical stuff menu
Return to Mathematical stuff menu

