Mad Teddy's web-pages

Martin Gardner's Borromean rings surface challenge

If you've arrived here by way of my A taste of topology page, you'll know how recreational mathematics guru Martin Gardner, in his book "Mathematical Puzzles and Diversions", issued a challenge to readers to produce a model made from paper (or some other thin material) of a surface bounded by three edges which bear the same relation to each other as the circles in the famous Borromean rings emblem:

- in which no two of the rings are linked, but all three are locked together.

You'll also have read how, in 1974, I did construct such an object, but that it didn't survive, and I forgot how I made it.

In mid-September 2005, 31 years after solving the challenge and making my first model, I've finally succeeded in producing another. This new model is in the same style as those shown in A taste of topology (i.e. made from play-dough); while it looks quite different from the model featured on this web-page (also mentioned earlier, but sadly no longer in existence as of 28th January 2011) and labelled "Minimum surfaces II", it's homeomorphic to it. Here it is:

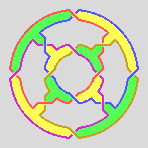
In the two small diagrams to either side of the photograph, the three colours red, blue, and purple are used to highlight the three edges / rings. You can see quite clearly that the relationship the edges bear to each other is as in the Borromean rings: locked, but not linked.

Also, notice that the surface is one-sided (like a Möbius strip). In the left-hand diagram, a single colour (green) is used to indicate this.

Having examined the model in the light of both the usual Borromean rings pattern, and also Minimum surfaces II (that page now defunct - see above), I made a further model which attempts to show the same concept but with threefold symmetry. This was the result:

It's a surprisingly simple structure. Considered as a solid object (a "manifold in 3-dimensional Euclidean space", to use the correct terminology), it has what topologists call "genus 3". This basically means it has three holes; more correctly, it's the number of cuts that would need to be made to remove all the holes, while still keeping the object as a single piece. (As mentioned in A taste of topology, topologists are sometimes described - rather rudely - as people who don't know the difference between a coffee cup and a doughnut, since both have genus 1.)

For comparison, here are all sixteen models presented in A taste of topology, with their genus numbers:

As you can see, models 7, 8, 15, and 16 all have genus 3, and are of comparable complexity to a surface with Borromean edges. (In fact, surfaces 13 and 14 are even more complex, each with genus 5.)

So I'm somewhat embarrassed that it's taken me so long to finally make a decent model of the Borromean surface!

Here's a question: is it possible to have a two-sided surface with three edges in the Borromean configuration?

I suspect that it's not possible, but I'm not sure. If anyone has made a model of such a surface, or can prove that no such surface exists, I'd be grateful if you'd contact me and let me know. I could then put the information here, and (if you wish) give credit to you for providing it.

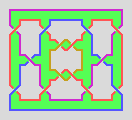
I've also made a model of a surface involving four rings:

(As you can see, I'm pushing my luck a bit here - play-dough is fine for reasonably simple exercises of this type, but things can start to get out of hand as the level of complexity goes up, especially with curved-edge models...)

Note that this arrangement of four rings is unlike the Borromean rings, in that the rings are linked as well as being locked. Also, notice that the surface is two-sided, and that the model has genus 5 (as in models 13 and 14, above).

It is possible to have four rings locked without being linked - in fact, it can be done with any number of rings. See this web-page to read more. (Check out some of the other web-links in this page - there's some good information here. One of these web-links leads to an mpeg movie which shows a set of six locked rings falling to pieces when one of the rings is cut - quite amusing. For convenience, here's that link.)

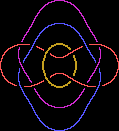
Here's my model of a surface whose edges are the "four-component Brunnian link" (see this page) - the true analogue of the Borromean rings involving four rings, locked but not linked:

This model has genus 7. Like the surface with three Borromean edges described earlier, it's one-sided.

I recommend also making a string model, using the diagram on the right as a guide. Then you can spend a very puzzling few minutes playing with it, and trying to get your head around exactly what's going on! I strongly suggest using four colours. Make the loops approximately equal in size (I made mine from 15cm lengths of string). The resulting artifact is, in its own way, just as intriguing as more familiar topological phenomena like Möbius strips and Klein bottles.

More questions to which I don't know the answers:

Is it possible to have a two-sided surface with four non-linked locked edges? (I suspect not...)

Can this be generalized to surfaces with any number of such edges? Specifically, will a surface with any number of non-linked locked edges always be possible, and will it always be one-sided if so? (I suspect that the answer is "yes" to both parts of this question...)

Plenty of food for thought there!

If you'd like to pursue knot theory and related matters further, and get some ideas for possible models of your own, I recommend the following links (all within one website):

http://www.knotplot.com/index.html

http://www.knotplot.com/knot-theory/

http://www.knotplot.com/zoo/
(In particular, check out the knot labelled 6³₂ to see an old friend...)

http://www.knotplot.com/various/AntoinesNecklace.html
(There's a connection here with the Cantor set. To read more about this, visit my Fractals #1: the Cantor and Mandelbrot sets page.)

Finally:

http://www.knotplot.com/knot-theory/torus_xing.html

Tons of stuff there to keep you out of mischief for a while!

Here's the (suitably nerdy) recipe I used to make my play-dough. If you'd like to make your own play-dough models, you may find it helpful. (It keeps quite well in a plastic bag in the freezer. )

PLAY-DOUGH

2 cups plain flour, C_mH_2nO_n
1 cup salt, NaCl
4 tablespoons cream of tartar, HOOCCH(OH)CH(OH)COOK
2 tablespoons cooking oil, C_mH_n
2 cups water, H₂O

Mix all the ingredients in a fairly large saucepan. Heat over
medium heat for 3-5 minutes, or until the mixture congeals.

>>>       Don't eat it!      It'll send your sodium levels sky-high!      <<<

Back to A taste of topology

Return to Mathematical stuff menu

My home page     Preliminaries (Copyright, Safety)